Metode Kuadrat Terkecil (Least Squares),kadang-kadang disebut analisis regresi, menentukan secara matematis garis yang paling sesuai,atau garis regresi linier, melalui sekelompok titik. Garis regresi meminimalisasi jumlah kuadrat deviasi dari setiap titik actual yang diplot dari titik di atas atau di bawah garis regresi. Tampilan 3-2 mengilustrasikan metode ini menggunakan data Barker Company, yaitu :

Ilustrasi metode perhitungan dalam menentukan elemen tetap dan variabel biaya
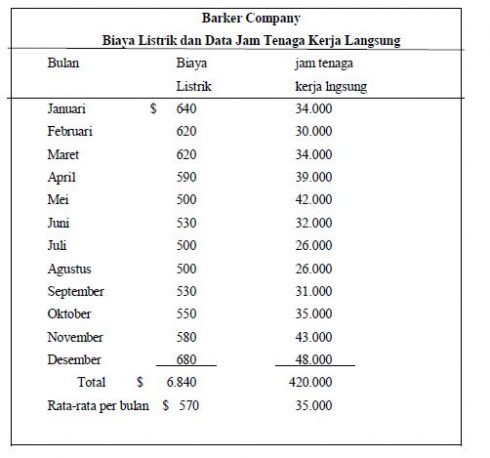
Untuk mempersiapkan table dilampiran 3-2 memerlukan langkah-langkah berikut:
1.Pertama, tentukan rata-rata biaya listrik, y, dan rata-rata jam teaga kerja langsung x. Tambahkan obsevasi di kolom 1 dan kolom 3, dan kemudian bagi dengan jumlah observasi. Rata-rata biaya listrik, y, adalah $ 570 ( $6840 total biaya listrik ÷ 12 bulan ). Rata-rata tenaga kerja langsung, x, 35.000 ( 420.000 total tenaga kerja langsung ÷ 12 bulan ).
2.Kemudian, hitung selisih dengan cara membandingkan biaya listrik actual bulanan , yi, dan jam tenaga kerja langsung actual bulanan, xi ; terhadap rata-rata bulanan masing-masing; rata-rata bulanan adalah y,dan x yang dihitung dilangkah 1. selisih ini dimasukkan di kolom 2 dan kolom 4 dan totalnya harus sama dengan nol,kecuali ada kesalahan dalam pembulatan.

Tampilan 3-2
Kemudian dua perkalian harus dilakukan. Pertama,kuadratkan setiap angka dikolom 4, (xi- x) ; masukkan hasilnya di kolom 5, (xi- x); dan totalkan kolom 5. kedua, kalikan setiap angka di kolom 4, (xi- x), dengan angka yang sesuai dikolom 2;maukkan hasilnya dikolom 6; dan totalkan kolom 6. ( perhatikan bahwa angka-angja dikolom 2 dikuadratkanjuga;hasilnya dimasukkan ke kolom 7 dan kolom 7 dototalkan. Total kolom 7 akan digunakan dalam bagian berikutnya untuk menhitung koefisien korelasi).
Tarif Variabel untuk biaya listrik ,b, dihitung sebagai berikut:

Hasil ini berbeda dengan hasil yang dihitung dengan metode scatterergraphkarena menyesuaikan suatu garis secara visual melalui titik-titik data tidaklah seakurat menyesuaikangaris secara matematis. Ketepatan mtematis dari metode kuadrat terkecil memberikan tingkat obyektifitas yang tinggi dalam analisis. Sebaiknya tetap berguna untuk memplot data guna melakukan verifikasi secara visual dependen dan variabel independen. Memplot data membuatnya leih mudah untuk melihat data abnormal yang dapatmendistorsi estimasi kuadratterkecil. Jika data abnormal ditemukan, data tersebut ebaiknya diekluarkan dari kelompok data sampel sebelum menggunakan rumus kuadrat terkecil. Dalam ilustrasi ini, ukuran sampel terlalu keciluntuk melakukan penyederhanan